Limites, conceitos fundamentais

Introdução

Em Física, como se sabe, utilizamos de uma poderosa arma: a Matemática. Não nos restringimos, naturalmente, à Matemática do Ensino Médio, mas, indo além, utilizamos amplamente do Cálculo, por exemplo. Pretendo, em breve, publicar um pequeno estudo sobre as Leis de Newton e, para tanto, irei necessitar do Cálculo, além de entidades matemáticas chamadas vetores. Para não deixar os leitores abandonados à própria sorte, antes do estudo das Leis da Dinâmica iremos estudar os pré-requisitos para compreender tais Leis. Começaremos isto hoje, neste artigo, introduzindo os conceitos de continuidade e limite de forma intuitiva; posteriormente tornaremos rigorosos esses conceitos, além de aprendermos um pouco sobre derivadas e, Cálculo à parte, também sobre os vetores. Não irei abordar o assunto em grandes detalhes, por questões de espaço; no entanto, tentarei apresentar um conteúdo satisfatório, além de, ao final, deixar recomendações para um estudo mais aprofundado. Também assumo, por parte do leitor, uma certa familiaridade com a Matemática elementar, principalmente com funções e o conjunto dos números reais, (1).

Continuidade e Limite

Sejam 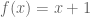 e .

Seus gráficos, respectivamente, são:

Gráfico da função 

e

Gráfico da função 

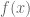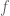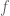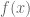Pode-se facilmente perceber que a linha que corta o gráfico de  segue ao longo dele sem nenhuma interrupção; ao contrário, a linha que corta o gráfico de  apresenta um “salto” no ponto . Pois bem: quando a linha que corta o gráfico de uma função  qualquer passa por um ponto  sem “saltar”, dizemos que a função  é contínua nesse ponto . Em nosso exemplo a função  é contínua em todo ponto  de seu domínio, ao passo que a função  não é contínua no ponto .

Agora, observemos o seguinte gráfico:

Noção de limite de uma função

Veja que quando  se aproxima de , então 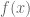 se aproxima de , de modo que quanto mais próximo de  estiver , mais próximo de  estará 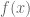; sem que, no entanto, . Dizemos, então, que o limite de 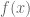, quando  tende a  é ; matematicamente:

Note que isso só acontecerá se a função 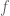 estiver definida e for contínua em . Do contrário ter-se-á que

Neste caso  é o valor que a função deveria ter para ser contínua no ponto dado.

Exemplos

Exemplo 1. Seja 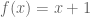. Ela é contínua no ponto 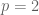? Calcule seu limite nesse ponto, caso exista.

Conforme vimos no primeiro gráfico ela é contínua em todo ponto  de seu domínio; logo, também em 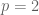. O valor de seu limite no ponto dado é, então

Exemplo 2. Seja . Ela é contínua em 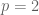? Calcule seu limite, caso exista.

Montando o gráfico podemos constatar que ela não é contínua em 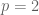 e, portanto, seu limite não existe nesse ponto; ou seja, . Devemos, então, encontrar o valor  que a função deveria ter para ser contínua em 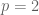. Fazemos isto, assim: para  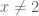temos que

,

visto que os termos iguais se cancelam. Portanto,

.

Conclusão

Espero que esta breve introdução aos fundamentos do Cálculo tenha sido suficientemente clara, agradável e útil. Espero também que os próximos artigos permaneçam assim, também. Para um estudo mais aprofundado, consulte os seguintes livros: